Algorithmique en classe de terminale
Généralités
Modalités de l’activité algorithmique
Comme
en seconde et en première, les trois modalités fondamentales de l’activité en
algorithmique en terminale sont :
-
analyser le fonctionnement ou le but d’un algorithme existant ;
- modifier un algorithme existant pour obtenir un résultat précis
-
créer un algorithme en réponse à un problème donné.
Contenus en termes d’algorithmique
Les instructions élémentaires sont toujours de 3 types : affectation, calcul, entrée, sortie.
Les élèves, dans le cadre d’une résolution de problèmes, doivent être capables :
-
d’écrire une formule permettant un calcul ;
-
d’écrire un programme calculant et donnant la valeur d’une fonction ; ainsi que les instructions d’entrées et sorties nécessaires au traitement.
Les autres éléments concernent les boucles, itérateurs et instructions conditionnelles :
Les élèves, dans le cadre d’une résolution de problèmes, doivent être capables de :
-
programmer un calcul itératif, le nombre d’itérations étant donné (boucle « pour »);
-
programmer une instruction conditionnelle ( « si…alors…sinon »), ou un calcul itératif avec une fin de boucle conditionnelle (boucle « tant que »
Capacités attendues
Dans le cadre de cette activité algorithmique, les élèves sont entraînés à :
-
écrire certains algorithmes en langage naturel ou dans un langage symbolique ;
-
en réaliser quelques-uns à l’aide d’un tableur ou d’un programme sur calculatrice ou avec un logiciel adapté ;
-
interpréter des algorithmes plus complexes
Une activité algorithmique peut avoir comme intention (même si d’autres outils peuvent être aussi pertinents) :
-
de développer ou de consolider des capacités en algorithmique attendues par le programme (calculer et afficher les termes d’une suite récurrente u n+1)= f(un));
-
d’introduire une notion (loi binomiale)
-
d’illustrer une notion (approximation de l’aire sous une courbe d'une fonction monotone sur un intervalle);
-
de créer des utilitaires ( second degré)
-
de résoudre un problème lié au programme (pour une suite croissante et non majorée (u n ) , calcul du rang n à partir duquel le terme dépasse une certaine valeur ;
-
de résoudre un problème transversal ( combien y a t il de segments joignant n points?)
Algorithmique dans les programmes de terminale S
Capacités attendues
![]() Suites :
Suites :
Dans le cadre d’une limite infinie, étant
données une suite croissante (un) et un nombre réel a, déterminer à l’aide d’un algorithme un rang à
partir duquel un>a.
![]() Intégration :
Intégration :
Pour une fonction
monotone positive, mettre en œuvre un algorithme pour déterminer un encadrement
d’une intégrale.
Commentaires
![]() Suites récurrentes(en particulier arithmético-géométriques) :
Suites récurrentes(en particulier arithmético-géométriques) :
Des activités algorithmiques sont menées
dans ce cadre.
![]() Fonctions :
Fonctions :
Des activités
algorithmiques sont réalisées dans le cadre de la recherche de solutions de
l’équation f(x)=k
![]() Probabilités et statistique
Probabilités et statistique
Des activités algorithmiques sont menées
dans ce cadre, notamment pour simuler
une marche aléatoire .
Conception et analyse d’algorithmes
![]() Algorithme 1
Algorithme 1
Ecrire un algorithme permettant de calculer le plus petit entier naturel n à partir duquel cette somme dépasse un nombre A donné.
![]() Algorithme 2
Algorithme 2
Une nouvelle chaîne du câble, possédant 4 000 abonnés estime qu’elle perd sur une région donnée 10 % de ses clients par trimestre.
Pour pérenniser l’entreprise, il lui faut atteindre 6 000 adhérents dans les 3 ans.
Elle décide donc de lancer une offre promotionnelle pour les nouveaux abonnés. Pour fixer le tarif de cette offre, elle a besoin de connaître le nombre minimum d’abonnements supplémentaires (chaque trimestre) nécessaires à sa survie.
Ecrire un algorithme qui affiche ce nombre.
![]() Algorithme 3
Algorithme 3
![]()
![]()
Interprétation et modification d’un algorithme
Analyse de l’algorithme papier fourni :
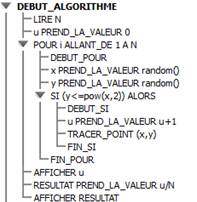
![]()
1)
Analyser l’algorithme ci-dessus. (Il peut être analysé en version
« papier » et/ou à faire tourner sur un logiciel : ) 2)
Adapter
cet algorithme afin d’approcher Cette méthode s’appelle la méthode de Monte-Carlo.![]()
Création de séquences intégrant l’algorithmique
![]() Situation 1 : racines en série…
Situation 1 : racines en série…
Etude d’une
suite définie par une somme.
![]() Situation 2 : un sot aléatoire…
Situation 2 : un sot aléatoire…
Un kangourou se trouve sur route déserte et graduée d’Australie occidentale, en un point. A chaque instant il saute d’un cran vers l’avant ou vers l’arrière avec la même probabilité.
On cherche à estimer le nombre moyen de passages au point de départ entre les instants 1 et 1 000.
Xcas version 2 avec appel d’un sous-programme
![]() Situation 3 : les balles populaires…
Situation 3 : les balles populaires…
Trois enfants Arnaud, Boris et Charles jouent à la balle.
Lorsque
![]() a la balle, la
probabilité qu'il l'envoie à
a la balle, la
probabilité qu'il l'envoie à ![]() est de
est de ![]() et la probabilité
qu'il l'envoie à
et la probabilité
qu'il l'envoie à ![]() est de
est de ![]() . Lorsque
. Lorsque
![]() a la balle, la
probabilité qu'il l'envoie à
a la balle, la
probabilité qu'il l'envoie à ![]() est de
est de ![]() et la probabilité
qu'il l'envoie à
et la probabilité
qu'il l'envoie à ![]() est de
est de ![]() envoie toujours la
balle à
envoie toujours la
balle à ![]() .
.
On
s'intéresse aux probabilités an, bn et cn,
des évènements « ![]() a la balle à l'issue
du
a la balle à l'issue
du ![]() ième lancer »,
«
ième lancer »,
« ![]() a la balle à l'issue
du
a la balle à l'issue
du ![]() ième lancer » et
«
ième lancer » et
« ![]() a la balle à l'issue
du
a la balle à l'issue
du ![]() ième lancer ».
ième lancer ».
Comme nous en avions discuté lors des différents stages, l’algorithmique a bien fait son entrée cette année dans les sujets de baccalauréat : Pondichéry (avril 2012)
Pour toute question, vous pouvez nous contacter à l’adresse : referentmath02@ac-bordeaux.fr